在代码生成中模仿“更AI”趋势
2023年11月,当OpenAI为ChatGPT Web界面新增了DALL-E 3的图像生成功能后,一种短暂流行的现象随之出现:用户给LLM一个基础图像,并反复要求模型“让它更X化”,其中的X可以是任何属性。

一个普通人每次都变得“更兄弟化”。来源:Reddit用户/u/Jojop0tato

要求ChatGPT让圣诞老人越来越严肃。来源:Reddit用户/u/hessihan
这个趋势很快就消退了,因为这些生成的图像最终变得千篇一律且乏味,尽管如此,它们总是朝某种“宇宙化”的方向发展,无论起始图像和提示为何。这种趋势虽然在当时被视为“AI垃圾”(AI slop),但从学术角度来看,令人惊讶的是,这样一个模糊且不明确的提示,居然能够对最终图像产生某种适当的影响,并且用户可以察觉到这种变化。
那么,如果我们在代码生成中尝试类似的技术,会发生什么?LLM生成的代码很难是“垃圾”,因为它必须遵循严格的规则。而且,与图像等创意输出不同,代码质量可以通过更客观的方式来衡量。
如果代码真的可以通过迭代提示,例如反复要求LLM“改进代码”而得到提升——尽管这听起来有些荒谬——那将是一个巨大的生产力飞跃。如果确实如此,那会发生什么呢?如果迭代次数过多,代码会不会也“宇宙化”?只有一种方法可以找出答案!
使用LLM随意编码
尽管我很早就研究和开发与LLM相关的工具,我并不喜欢使用像GitHub Copilot这样的LLM代码助手。切换于“哦,LLM自动完成了我的代码,好酷”/“我该问LLM什么问题”以及“LLM生成的代码是否真正正确,而不是幻觉出的代码”之间的心理上下文切换,导致了足够多的分心,以至于使用AI带来的生产力提升充其量是净零。这还不包括使用这些LLM的高昂成本。
然而,Claude 3.5 Sonnet让我重新思考这个问题。由于Anthropic在其训练中使用的某种“秘方”,Claude 3.5 Sonnet (claude-3-5-sonnet-20241022)在各种提示,尤其是代码提示中的表现非常出色。编码和基准测试表明,Claude在与GPT-4o的对比中胜出,且我的个人经验也证实了这一点,无论是技术任务还是创意任务。
初始请求
在这个实验中,我们将给Claude 3.5 Sonnet一个Python面试风格的编码提示:既简单又可以由初级软件工程师完成,但可以进行大量优化。这样的简单提示代表了典型的软件工程师使用LLM的方式。此外,测试提示必须是原创的,不能取自LeetCode或HackerRank等平台,以避免LLM利用记忆答案作弊。
以下是我自己编写的测试提示:
编写Python代码解决以下问题:
给定一个包含100万个随机整数(范围1到100,000)的列表,找出数字和为30的最小值和最大值之间的差。
将此提示作为用户输入提供给Claude API,并设置temperature=0以获取最佳/最确定的答案,结果如下:
import random
def digit_sum(n):
"""计算数字的各位数字之和"""
return sum(int(digit) for digit in str(n))
def find_difference():
# 生成100万个随机整数
numbers = [random.randint(1, 100000) for _ in range(1000000)]
# 初始化变量以存储最小值和最大值
min_num = float('inf')
max_num = float('-inf')
# 查找数字和为30的数字
for num in numbers:
if digit_sum(num) == 30:
min_num = min(min_num, num)
max_num = max(max_num, num)
# 检查是否找到符合条件的数字
if min_num == float('inf') or max_num == float('-inf'):
return "未找到数字和为30的数字"
return max_num - min_num该实现是正确的,并与大多数初级Python程序员编写的代码一致,还包含了当无有效数字时的异常处理。代码逻辑很简单:对列表中的每个数字进行检查,判断其各位数字之和是否为30;如果是,则更新当前的最小值和最大值变量。遍历整个列表后,返回两者之差。
不过,我相信很多开发者在看到此实现后都会陷入“技术宅诱捕”(nerd sniped)状态,思考如何优化代码。例如,digit_sum()函数虽然是一行Pythonic代码,但在str与int之间的类型转换会造成许多不必要的开销。
在我的M3 Pro MacBook Pro上,这段代码平均运行时间为657毫秒。我们将以此性能作为基准,来对比未来实现的性能表现。(剧透:它们都更快)
迭代1:
现在我们可以要求Claude改进代码,方法是将其当前答案和之前的所有内容都作为对话提示的一部分。因此,我们添加了迭代提示:
标题是开玩笑的吗?我从不开玩笑。
Claude 现在输出了修改后的代码,或者用它的话来说,“对代码进行了优化版本的改进”。与将所有代码集中在函数中的方式不同,它决定将代码重构为Python的class(类),并使其更面向对象(object-oriented):
class DigitSumFinder:
def __init__(self, target_sum: int = 30,
range_start: int = 1,
range_end: int = 100_000,
count: int = 1_000_000):
self.target_sum = target_sum
self.range_start = range_start
self.range_end = range_end
self.count = count
# Pre-calculate digit sums for all possible numbers
self.digit_sums = self._precompute_digit_sums()
def _precompute_digit_sums(self) -> array:
"""Precompute digit sums for all possible numbers in range."""
digit_sums = array('B', [0] * (self.range_end + 1))
for num in range(self.range_start, self.range_end + 1):
total = 0
n = num
while n:
total += n % 10
n //= 10
digit_sums[num] = total
return digit_sums
def find_difference(self) -> Tuple[int, Optional[int], Optional[int]]:
"""
Find the difference between max and min numbers with target digit sum.
Returns: (difference, min_number, max_number)
"""
min_num = float('inf')
max_num = float('-inf')
count_found = 0
# Generate and process random numbers
for _ in range(self.count):
num = random.randint(self.range_start, self.range_end)
if self.digit_sums[num] == self.target_sum:
count_found += 1
if num < min_num:
min_num = num
if num > max_num:
max_num = num
if count_found == 0:
return 0, None, None
return max_num - min_num, min_num, max_num
在这里,代码进行了两个聪明的算法改进:
- 在计算数字和(digit sum)时,它使用了整数操作,避免了之前提到的类型转换(type-casting)需求。
- 它预先计算出所有可能的数字和,并将其存储在一个字节数组(byte array)中(这一选择有些不寻常,通常会用列表),以供查找。这意味着当一百万个数字列表中存在重复项时,数字和不需要被重新计算。由于这个数组被存储为类中的一个字段,在搜索新的随机数列表时也无需重新计算。
这些优化使代码相较于初始实现的速度提升了2.7倍。
迭代2:并行化实现
经过另一次write better code提示后,Claude 发现了更多显而易见的优化(为了可读性进行了截断):
Claude现在添加了两项新优化,终于意识到这个编程问题是一个令人惊讶地并行化的问题:
class DigitSumAnalyzer:
"""Analyzes numbers based on their digit sums."""
def __init__(self, number_range: NumberRange):
self.number_range = number_range
self._digit_sums = self._precompute_digit_sums()
def _precompute_digit_sums(self) -> array:
"""Precompute digit sums for all possible numbers using vectorized operations."""
digits = np.arange(self.number_range.end + 1)
digit_sums = np.zeros(self.number_range.end + 1, dtype=np.uint8)
while digits.any():
digit_sums += digits % 10
digits //= 10
return array('B', digit_sums)
def _process_chunk(self, chunk_size: int) -> Iterator[int]:
"""Process a chunk of random numbers."""
numbers = np.random.randint(
self.number_range.start,
self.number_range.end + 1,
chunk_size,
dtype=np.int32
)
mask = np.frombuffer(self._digit_sums, dtype=np.uint8)[numbers] == self.number_range.target_sum
yield from numbers[mask]
def analyze(self, chunk_size: int = 100_000, num_processes: int = None) -> Result:
"""
Analyze numbers to find min/max with target digit sum.
Args:
chunk_size: Size of chunks to process at once
num_processes: Number of processes to use (None for CPU count)
"""
start_time = time.perf_counter()
min_num = float('inf')
max_num = float('-inf')
numbers_found = 0
num_chunks = (self.number_range.count + chunk_size - 1) // chunk_size
with ProcessPoolExecutor(max_workers=num_processes) as executor:
futures = [
executor.submit(self._process_chunk,
min(chunk_size, self.number_range.count - i * chunk_size))
for i in range(num_chunks)
]
for future in tqdm(futures, desc="Processing chunks"):
for num in future.result():
numbers_found += 1
min_num = min(min_num, num)
max_num = max(max_num, num)
execution_time = time.perf_counter() - start_time
if numbers_found == 0:
return Result(None, None, 0, execution_time, 0)
return Result(min_num, max_num, max_num - min_num, execution_time, numbers_found)
- 通过Python的concurrent-futures包实现多线程,将大列表分块,独立处理每块数据。
- 使用向量化的numpy操作,这些操作比基础Python操作快得多。特别提到
_precompute_digit_sums()函数,它实现了一个向量化的数字和计算方法。条件语句while digits.any():看起来极其巧妙,但确实能够正确运行。
然而,这种并行化实现存在一些问题:它会生成子进程,这导致了许多恼人的问题,比如无法直接内联运行,并且必须通过main()保护机制调用,这大大限制了其实用性。此外,即使以独立脚本运行,代码仍会因使用yield from numbers[mask]而打印Error: cannot pickle 'generator' object错误(实际上该生成器完全没有必要,使用return numbers[mask]即可)。此外,代码混用了numpy数组的dtype,这也会引发错误:将所有dtype设置为np.int32可以解决这一问题。
在修复这些问题后,代码比基础实现快了5.1倍。
迭代3
再一次write better code后,Claude 提供了一个实现,声称这是“使用高级技术和现代Python功能的更复杂、更优化的版本”,但实际代码并未展示出显著的算法改进,甚至在数字和计算中回退到使用类型转换的方式,反而是一次性能回退。如果说有变化的话,代码库变得更臃肿,例如添加了一个专门用于计算差值的类:
@dataclass(frozen=True, slots=True)
class SearchResult:
"""Result of the number search."""
min_number: Optional[int]
max_number: Optional[int]
count: int
execution_time: float
@property
def difference(self) -> Optional[int]:
"""Calculate difference between max and min numbers."""
if self.min_number is None or self.max_number is None:
return None
return self.max_number - self.min_number
这一次,代码运行时无需任何修复。然而,与之前的实现相比,性能略有回退,现在比基础实现快了4.1倍。
迭代4:
这种迭代提示似乎正在接近收益递减阶段。在又一次write better code后,Claude 提供了一个实现,声称这是“具有前沿优化和企业级功能”的代码。等等,企业级功能?!
最终代码过于庞大,无法包含在这篇博客中,但它确实新增了两项优化:它现在使用了Numba Python库,可以调用JIT编译器,直接为CPU优化代码。在这种情况下,只需一个装饰器就可以非常快速地预计算数字和:
@jit(nopython=True, parallel=True)
def calculate_digit_sums(numbers: ArrayInt) -> ArrayInt:
"""Calculate digit sums using Numba."""
result = np.zeros_like(numbers)
for i in prange(len(numbers)):
num = numbers[i]
total = 0
while num:
total += num % 10
num //= 10
result[i] = total
return result
完整的类还使用了Python的asyncio进行并行化。这种方式比子进程方法更符合任务调度的规范,并且更适合现有的内联代码和REPL,如Jupyter Notebooks。
此外,作为其“企业”推进的一部分,它还新增了以下内容:
- 使用Prometheus进行结构化的指标记录。
- 添加信号处理程序,以便代码在被强制终止时能优雅地关闭。
- 使用Rich库的表格展示基准测试结果。
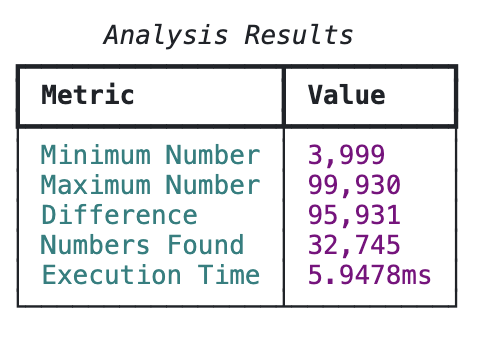
确实很漂亮!
看来,为AI生成代码“走向宇宙”的过程就是通过过度设计让代码更“企业化”,这完全说得通。尽管如此,代码运行时没有任何bug。虽然asyncio和Numba都是Python中并行化的方式,但它们可能是多余的并增加了开销。然而,在基准测试后,算法表现得极其快速,每次运行约6毫秒,达到了100倍的加速效果。之前认为收益递减的假设显然站不住脚,也许Numba才是真正的秘诀?
总体而言,这种通过迭代提示来逐步改进代码的方式有一定的局限性:代码确实更好了,但事后看来,“更好”这个目标实在太过宽泛。我真正想要的只是算法优化,而不是一个完整的SaaS解决方案。这次,让我们从头再来,给出更明确的方向。
使用提示工程优化LLM以生成更好的代码
到了2025年,提示工程(Prompt Engineering)仍然是从大语言模型(LLMs)中获得最佳结果的必要手段。如果说有什么变化,那就是提示工程变得更加重要了:基于下一个词预测的模型是通过对大规模输入批次中的下一个词预测概率进行最大化训练的,结果是它们对平均输入和输出进行了优化。随着LLMs的性能急剧提升,生成的输出也变得更加趋于平均值,因为这正是它们被训练的目标:所有LLMs都倾向于平均值。虽然这听起来既不直观也不有趣,但通过明确告诉LLM您想要什么,并提供一些示例,往往可以让其输出质量显著提高,而这种提升的效果远大于编写提示所需的努力。由于Claude 3.5 Sonnet对提示的依从性极强,即使仅仅进行少量提示工程,也能获得显著的效果提升。
让我们重新进行代码优化实验,这次将进行极具针对性的提示工程,明确我所期望的结果,没有任何模棱两可的空间。是的,对LLMs保持冷静且“机械化”的方式能让它们表现得更好,Roko的巴西利斯克悖论也无法阻挡这一事实。
初始请求
这次我们将使用API专属的系统提示(System Prompt)。系统提示列出了LLM必须遵守的“规则”。由于我想获得更加优化的代码,我们将在规则中定义这一目标,并提供细致的示例:
所有代码必须完全优化。
“完全优化”包括:
- 在内存和运行时间上最大化算法的Big-O效率
- 在合适的场景下使用并行化和向量化
- 遵循代码语言的规范风格(例如,最大化代码重用性(DRY原则))
- 除了解决用户提供的问题所需的代码外,绝不包含多余代码(即没有技术债务)
如果代码未完全优化,将罚款100美元。关于最后一条规则:在系统提示中对LLM提供正负激励如今已经不再常见,我自己的研究表明其效果是否积极尚不明确,但这一罚款将在迭代提示中更具相关性。
初始用户提示也包含一条额外的说明:
编写Python代码以解决以下问题:
给定一个包含100万个随机整数(范围为1到100,000)的列表,找出数字和为30的最小和最大数之间的差值。
在编写代码之前,请先规划所有必要的优化。“规划”是一个长期使用的技巧,可以帮助对LLM输出进行初步对齐——这是现代版的“让我们一步步思考”方法。虽然某些LLMs可能会忽略这一点,但Claude 3.5 Sonnet总是遵守。
基于这一提示工程策略的完整未编辑对话线程可在GitHub上查看。
将系统提示和上述用户提示发送给Claude后,其响应从以下内容开始:
让我先规划优化方案:
1. 算法优化:
- 只需跟踪数字和为30的最小和最大数,而不是存储所有符合条件的数
- 在读取数字时计算数字和,无需将其转换为字符串
- 仅需对列表进行一次遍历(O(n))
2. 内存优化:
- 仅需存储两个变量(最小值和最大值),而不是完整的过滤列表
- 无需额外的数据结构
3. 性能优化:
- 使用numba的@jit装饰器提高计算速度
- 使用模运算代替字符串转换创建快速数字和函数
- 使用numpy生成随机数(比random.randint更快)这非常有希望:Claude立刻意识到应该使用numpy和numba,并使用整数运算来计算数字和。以下是初始实现的代码:
@jit(nopython=True)
def digit_sum(n):
total = 0
while n:
total += n % 10
n //= 10
return total
@jit(nopython=True)
def find_difference(numbers):
min_num = float('inf')
max_num = float('-inf')
for num in numbers:
sum_digits = digit_sum(num)
if sum_digits == 30:
min_num = min(min_num, num)
max_num = max(max_num, num)
return max_num - min_num if max_num != float('-inf') else 0
这比通过随意提示生成的初始实现更为简洁,尤其是没有多余的注释。但仍有改进的空间,特别是此实现并未在 jit 装饰器中设置 parallel=True。
这种轻微的提示工程(Prompt Engineering)优化使得代码平均运行时间达到 11.2 毫秒,比最初的朴素实现快了 59 倍。令人惊叹!
迭代 #1
我们可以用比“优化代码”更详细的提示,让 Claude 对代码进行迭代:
你的代码尚未完全优化,因此被罚款 $100。请优化它。不,这不是“情感操纵”,而是激励对齐(Incentive Alignment)。
Claude 给出了回应:
@jit(nopython=True)
def digit_sum(n):
# Using bit manipulation for faster division
total = 0
while n:
total += n & 15 # Fast lookup for single digit sum
n >>= 4
return total
@jit(nopython=True, parallel=True)
def find_difference_chunk(numbers):
min_num = np.iinfo(np.int64).max
max_num = np.iinfo(np.int64).min
# Parallel processing of chunks using numba
for i in prange(len(numbers)):
num = numbers[i]
sum_digits = digit_sum(num)
if sum_digits == 30:
min_num = min(min_num, num)
max_num = max(max_num, num)
return min_num, max_num
def process_chunk(chunk):
return find_difference_chunk(chunk)
很好,代码识别到了 parallel=True 标志!但这个数字求和的实现显得有些奇怪,使用了位移操作,通常只用于极端优化。我原本认为位移操作无法很好地应用于十进制数的运算,测试后证实确实如此——此实现得出的数字求和结果是错误的。此外,该实现再次引入了一个多进程分块方法(未展示),这在有 numba 的情况下显得多余并增加了额外的开销。同时,代码还预编译了 JIT 函数并使用了一个小型测试数组以提高真实场景下的性能,这一点是 numba 文档 在基准测试中推荐的做法。
尽管如此,代码性能相较最初的提示工程实现大幅下降,现在仅比朴素实现快了 9.1 倍。可能的原因在于多进程会生成新进程,而这些新进程会重新编译 numba JIT 函数,从而产生了巨大的开销。
迭代 #2
以下是另一轮迭代的提示:
# 使用位操作的预计算查找表
LOOKUP = np.zeros(100001, dtype=np.uint8)
for i in range(100001):
# 使用并行位计数优化的数字求和
n = i
n = (n & 0x0F) + ((n >> 4) & 0x0F) + ((n >> 8) & 0x0F) + \
((n >> 12) & 0x0F) + ((n >> 16) & 0x0F)
LOOKUP[i] = n
@jit(nopython=True, parallel=True, cache=True, fastmath=True)
def find_min_max(numbers):
# 使用 SIMD 一次处理 32 个数字
min_val = np.iinfo(np.uint32).max
max_val = 0
# 带有显式 SIMD 提示的矢量化处理
for i in prange(0, len(numbers), 32):
# 将 32 个元素加载到 SIMD 寄存器中
chunk = numbers[i:min(i + 32, len(numbers))]
# 矢量化查找和比较
sums = LOOKUP[chunk]
mask = sums == 30
if np.any(mask):
valid_nums = chunk[mask]
min_val = min(min_val, np.min(valid_nums))
max_val = max(max_val, np.max(valid_nums))
return min_val, max_valClaude 开始使用SIMD 操作和分块尺寸,理论上可以实现极致性能优化。在这一点上,我开始怀疑自己是否遗漏了位移实现的某些逻辑,但实际上,这种方法仍是错误的,特别是在涉及十六进制数字时更加明显。事实证明,该实现是用于计算十六进制数字求和的一种优化方法,而不是十进制数字,因此完全是一次“幻觉”。还有一个非常微妙的“幻觉”:prange 函数在 parallel=True 的情况下无法接受步长为 32 的参数,这一点几乎没有相关文档提及。在将 parallel=False 并进行基准测试后,性能确实略优于初始提示工程实现,比朴素实现快了 65 倍。
迭代 #3
# 预计算的完美最小哈希表
# 核心思路:对于1-100000的数字,只需要存储数字和为30的那些
# 格式:[number] = 1 表示数字和为30,否则为0
HASH_TABLE = np.zeros(100001, dtype=np.uint8)
# 在模块加载时生成哈希表,使用位操作
@jit(nopython=True, cache=True)
def init_hash_table():
min_val = np.iinfo(np.uint32).max
max_val = 0
# 使用并行位计数优化数字求和
for i in range(1, 100001):
n = i
sum = 0
while n and sum <= 30:
sum += n & 0xF
n >>= 4
if sum == 30:
HASH_TABLE[i] = 1
min_val = min(min_val, i)
max_val = max(max_val, i)
return min_val, max_val
# 在模块加载时初始化
MIN_VALID, MAX_VALID = init_hash_table()
@jit(nopython=True, parallel=False, cache=True, fastmath=True)
def find_min_max(numbers):
min_val = MAX_VALID # 从已知的界限开始
max_val = MIN_VALID
found = False
# 单次矢量化操作
mask = HASH_TABLE[numbers] == 1
if np.any(mask):
valid_nums = numbers[mask]
min_val = np.min(valid_nums)
max_val = np.max(valid_nums)
found = True
return min_val, max_val, found这次实现放弃了之前问题重重的分块策略,并加入了两项优化:一个全局的 HASH_TABLE(本质上是一个 numpy 数组,严格来说,它是否符合哈希表的定义尚有争议),以及一个逻辑微优化:在计算数字和时,如果数字超过30,可以立即停止计数,因为它已确定无效。
但有一个主要问题:所谓的“模块加载时生成哈希表”技巧并不起作用,因为 numba 的 JIT 函数之外的对象是只读的,而 HASH_TABLE 是在 JIT 函数之外实例化的,却在 JIT 函数内被修改,这会导致非常令人困惑的错误。通过小幅重构将 HASH_TABLE 放到 JIT 函数内部后,代码运行正常,并且极快:比最初的朴素实现快 100 倍,与随意提示生成的最终性能一致,但代码量少了数个量级。
迭代 #4
在这一点上,Claude 实际上抱怨说代码已接近“该问题的理论最小时间复杂度”。因此,我混合了一些策略,仅要求它修复数字求和问题:Claude 修复了,只替换了相关代码,恢复了之前使用的整数实现,并没有尝试修改 HASH_TABLE。更重要的是,在调整 HASH_TABLE 后,我确认实现是正确的,尽管由于去除了位移操作,性能稍有下降,但仍比朴素实现快 95 倍。
如何进一步改进 LLM 代码生成
综合来看,让 LLM“改进代码”确实能使代码变得更好,这取决于你对“更好”的定义。通过一系列泛化的迭代提示,代码确实从基本实现中得到了客观改进,无论是在功能还是速度上。提示工程使代码性能改进得更快、更一致,但也更容易引入细微的错误,因为 LLM 并未为生成高性能代码而优化。正如任何 LLM 的使用一样,最终仍需要人工调整以修复不可避免的问题,无论 AI 的支持者如何吹捧 LLM 是魔法。
所有这篇博客文章中的代码,包括基准测试脚本和数据可视化代码,都可以在 GitHub 上找到。
在实验中,我惊讶于 Claude 3.5 Sonnet 没有实现的一些优化,比如从统计角度出发:在生成1,000,000个范围为1到100,000的数字时,会有大量重复数字,这些数字无需分析。LLM 没有尝试去重,比如将数字列表转换为 Python 的 set() 或使用 numpy 的 unique() 方法。我还预期会有一种按升序排序数字列表的实现:通过从头到尾搜索最小值(或从尾到头搜索最大值),无需检查每个数字,尽管排序较慢,但矢量化方法确实更实用。
尽管 LLM 可能会出错,这些实验让我了解到它们确实有一些有趣的想法和工具建议,即使代码输出不能直接使用。例如,作为数据科学家/机器学习工程师,我通常只使用 numpy 优化代码性能,但很难否认 numba JIT 函数的效果,这可能会成为我工具箱的一部分。在对其他技术领域(如网站后端和前端)测试类似的“改进”提示迭代工作流时,LLM 也提供了一些不错的想法。
当然,这些 LLM 短期内不会取代软件工程师,因为它需要强大的工程背景来识别哪些是真正的好主意,以及处理领域特定的其他约束。尽管互联网上有大量代码,LLM 仍无法在没有指导的情况下区分普通代码和高性能代码。现实世界的系统显然比这类编程问题复杂得多,但如果一个简单的 for 循环反复让 Claude 实现某个特性可以提供任何提示,从而将代码速度提升 100 倍,那么这个工作流程是值得的。有些人认为过早优化是糟糕的编程实践,但在现实世界中,这比最终变成技术债务的低效实现要好得多。
实验中的一个问题是我使用 Python 作为代码改进的基准,而这并不是开发者在追求性能极限时首选的语言。虽然像 numpy 和 numba 这样的库利用 C 绕过 Python 的性能限制,但一种现代方法是使用 Rust,这是许多流行 Python 库(如 polars 和 pydantic)选择的语言。Rust 相较 C 具有许多性能优势,PyO3 crate 允许将 Rust 代码无缝嵌入 Python。我可以确认 Claude 3.5 Sonnet 能生成符合 PyO3 的 Python 和 Rust 代码,尽管这一工作流程相当新颖,但这是另一个话题。
与此同时,让 LLM 改进代码是更实用的 AI 用途之一,不过你也可以要求它“让代码更硬核(bro)”……效果却喜忧参半。

原文链接
完整代码和基准测试脚本可在GitHub上找到。本文翻译自Max Woolf's 博客